 |
杉原剛介 |
 |
杉原剛介 |
[Summary]
Chemical thermodynamic studies on micelle formation of various types of surfactants such as anionic, cationic and nonionic surfactants were overviewed paying special attention to the solution properties as functions of concentration C, temperature, T and pressure P. The correlationship between the critical solution pressure (CSP, Tanaka pressure) and the critical solution temperature (CST, Krafft temperature) was indicated in the three dimensional phase diagram of C, P and T for ionic surfactants. Chemical thermodynamic equations of the Gibbs free energy ΔGmo , enthalpy ΔHmo , entropy ΔSmo and volume changes ΔVmo upon micelle formation from singly dispersed as well as hydrated solid states were introduced and how to determine these thermodynamic parameter was demonstrated for different surfactants on the basis of the both models of micelle formation, i.e., the mass action model (MAM) and the phase seperation model (PSM).
キーワード:イオン性/非イオン性界面活性剤、ミセル形成の熱 力学、臨界ミセル濃度(CMC)、臨界溶解温度(CST, Krafft Temperature)、臨界溶解圧力(CSP, Tanaka Pressure)
一つの分子に、疎水基hydrophobic groupと親水基hydrophilic groupを併せ持つと、その分子は油に対しても、水に対しても溶解性を増すことが考えられる。したがって、このような物質が、水に溶存する場合、食塩やショ糖が溶存する状態とは異なるであろうことが当然予想される。すなわちそれが溶けて行くと、元来、水に溶け難い疎水基の部分を、気-液界面につきだして、その界面にびっしりと並ぶようになる。この界面に集合する現象を吸着adsorptionと呼ぶ。吸着が起こると、その水溶液の表面張力は著しく下げられる(図1参照)。少量の添加で液体の表面張力を著 しく低下させる物質を界面活性剤surfactantと呼び、その機能を界面活性surface activeであるという。一般に、同一分子内に極性基と非極性基を有する場合、多かれ少なかれ、界面活性となる。
さて、さらに活性剤(界面活性剤を簡単にこう呼ぶことにす る)の濃度を増して行くと界面が飽和吸着状態に近づき、一方、液相中の活性剤は、数個ないし数十、あるいは数百個の分子が、疎水基と水との接触を最小限にするように、疎水基を内側にして集合し、エネルギー的に安定な状態を取り始めるようになる。この集合によって、一つの粒子を形成することを、活性剤のミセル形成micellization、またはmicelle formationと呼び、その粒子をミセルmicelleと呼ぶ。界面活性剤の代表的なものは、石鹸soap や洗剤detergentであり、これらのミセルは数十~数百程度のも のが会合associationして作られるのが普通である。しかし、生 体の活性剤である胆汁酸塩などは、洗剤とは異なり、2個、3個、 ………のオリゴマー的自己会合self-associationから始まるものが多く、通念的なミセルとは区別しようとする考えもある。ここでは、ミセルを広義に解釈して、二量体、三量体 (dimer, trimer) 程度の自己会合体も含ませることにする。もし、適当な活性剤の水溶液中に、微小な油滴をつくると、その油滴表面にも活性剤の吸着が起こり、その油滴を水溶中に分散dispersionさせることができる。油滴を活性剤が分散させている状態を乳化emulsionといい、これは活性剤の重要な機能の一つである。乳化の状態は、エ ネルギー的(熱力学的)には安定ではない。これとよく似た状態 で、ミセル中に疎水性物質が少量溶解して活性剤と共に安定な集合状態をとっていることを可溶化solubilizationしているという。 可溶化状態は熱力学的に安定な状態であるために、活性剤の性質 を議論する上で重要である。
濃度が増加して、ミセルができ始める臨界濃度を臨界ミセル濃 度critical micellization concentration (CMC) と呼ぶ。このCMCは、普通の洗剤では鋭敏に観測できるものであるが、胆汁酸塩のようにオリゴマーoligomerから徐々に会合数aggregation またはassociation numberを濃度と共に増していく性質のあるものは、CMCの決定が困難であり、測定法によって著しく異なっ た値がでてくるおそれがある。しかし、CMCを決定することは、 界面活性物質を調べる上で、最も基本的なことがらで、欠くこと のできないものである。なぜなら、CMCは熱力学に直接関係づけ られる、最も重要なパラミターであるからである。
ミセルを論じるとき、CMC以外にミセルの形状(形と大きさ)、 表面の状態及び内部の状態を含めて、ミセルの構造を知らねばな らない。後でこれらについて述べて行くことにして、ここでは、ミ セル形成に直接関係のある因子を列挙すると、
①疎水基の大きさとその化学構造
(炭化水素部分の炭素数はいくつか、鎖状かあるいはステロイド
のような面構造かなど)
②親水基の種類
(非イオン性かイオン性か、イオン性であれば、カチオンかアニ
オンか、解離基や反対イオンは何かなど)
③添加物の有無
(添加塩の種類と濃度、アルコール類の種類と濃度など)
④温度と圧力
などである1)。
この総説記事においては、同仁化学研究所が製造している膜蛋白質可溶化剤としての活性剤各種を含めて、いろいろなタイプ の活性剤の水中におけるミセル形成について論じよう。
1. 界面活性剤水溶液物性における化学熱力学の概要
具体的な実例に基づいてミセル形成を論じる前に、ここでは先 ずその熱力学の骨子を述べておこう。理論を詳細に論じたものと して、古くよりShinodaによるColloidal Surfactantsと題する成書がよく引用されて来た2) 。また、日本語で書かれたものに、田中が分担執筆した「応用コロイド科学」なる成書 3)や総説4)がある。今ではさらに完成度を高め、参照にも極めて有用な成書 "Micelles" がMoroiによって著されている5)。本節は、Moroiが極めて厳密に一般化して議論したものに基づいた著者らの総説6)などを、さらに単純化して紹介する。
1.1. イオン性活性剤のミセル形成―Mass Action Model
先ずイオン性活性剤としては、活性剤イオンをS- で表し、反対イオンをNa+とするナトリウム塩NaSを考える。会合数n i個が集合してできたミセルをMiで表し、これにm i個の反対イオンがミセル表面に吸着して、ミセルに対して静電的安定化をもたらしてい るとする。ミセルの会合数は多分散であることが知られており、水 中では次の様な平衡状態にある。
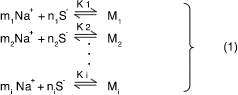
また、溶液全体は電気的に中性であるから、ミセルと平衡にあって単分散状態にあるNa+ とS- の濃度を[Na+]と[S-]でそれぞれ表し、これらと平衡にあるミセル濃度を[Mi ]で表すと次式が成立たねばならない。
![]()
式(1)からミセル化定数Kiは次式で表される。
![]()
ここで議論を簡単にするため、ミセル会合数の分散は考えないでnに固定されたもの(nを会合数の平均値とみなしてよい)とす る。したがって会合数nのミセル濃度[Mn]は次式で与えられる。
![]()
さらに活性剤の総濃度をCtで表すと式(1)と(4)より次式を得る。
![]()
この式(5)からミセル1個につき吸着した反対イオンの結合度( βでしばしば表される)m/nは次のようになる。
![]()
一方、式(4)の対数をとると
![]()
この式から β = m/nの値はln[S-]をCMC以上でln[Na+ ]に対してplotするとその勾配そのものがβであることがわかる。何故ならlnKnに比べてln[M n]は無視できるほど小さいからである。
式(7)は(5)を用いれば次のように書き換えられる。
![]()
ここでMoroiはSodium dodecylsulfate (SDS) に対する実験で、ln[S-]対ln[Na+ ]のplotで直線関係が成立つことを示し、式(7)や(8)に現れる三つのパラミターの値を決めることが出来た。 すなわち、Kn = 230, n = 64及びm = 46.7 (∵ β = 0.73) を得、さらに、bulk濃度[S-]と[Na+ ]が、ある与えられた活性剤濃度で式(8)を使って求められることを示した。 5), 7) また、実験に基づいて、CMCにおいては、[S-]や[Na+]の値が活性剤総濃度の99%以上であることや、ln[M]の値がlnKnの値の3%以下であることなどを結論づけている。これらのことからCMC値 の対数値を反対イオン濃度の対数値に対してplotすると、よい直線関係が得られ、その勾配から β = m/nの値が良い近似で求められることを示した。
![]()
ここで [Na+] は添加塩がNaCl であればその濃度と活性剤由来のNa+との和であるので、[Na+]= CMC +[NaCl]で表されるものである。式(9)が直線関係で表されることは多くの文献で報告 されており8-15)、なかでも最初の発見者の名をとって ln CMC vs ln [Na+] の plot を Corrin - Harkins Plotと呼んでいる。この方法による反対イオン結合度 β の決定は今も盛んに応用されている15-19)。
会合数にばらつきのないイオン性活性剤のミセルに対しては、 CMC近傍で次の二つの式が成立つことが示された5) 。

この平衡定数から活性剤イオン1molあたりの標準Gibbsエネル ギー変化は、それぞれの標準化学ポテンシャル(無限希釈を基準 とする)で示せば、
![]()
であるが、nΔGo = -RTlnKn でもあることから、次式で示される。ただし、式中のXCMCはモル分率で表したCMC値である。
![]()
ここでm/n = β であることを思い出して、ΔGoに対応するエンタ ルピーおよびエントロピー変化はそれぞれ
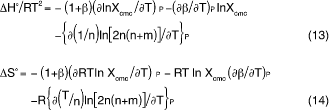
で表される5)。ミセル形成の熱力学的パラミターには、 ΔSoやΔHoのほかに体積変化ΔVoがある。これは体積Vが圧力Pと共役関係であることから、すなわち(∂DG/∂P)T = ΔVであることより、式(12)をT = const.の条件で圧力Pで偏微分すれば得られる。(ここで ΔSoやΔHoの関係式の中に反対イオン結合度β と会合数nの温度変化に対応する項が第2項と第3項としてそれぞれ含められていることに注目しておこ う。)ΔVoについてはCMCの圧力依存性のところでも述べる。以上は1-1電解質型の活性剤について述べたものである。
1.2. 非イオン性活性剤のミセル形成
― Mass Action Model
では非イオン性の活性剤ではどうかというと、上と同様に会合 数nに分布がないものとし、非イオン性活性剤分子をSで表すと nS <-> M の平衡が成立っている。この状況に対して、ミセル形成の標準Gibbsエネルギー変化は
![]()
である。Moroiの厳密な表現から出発して、n > 50の範囲(実際のミセルの会合数はこの範囲のものが多い)で成立つΔGoは、次式のように近似的な表現ができる 5)。
![]()
この式をもとに、ΔSoやΔHoが次のように表されることを記しておく。(以下の式の中にも、CMCの温度変化だけでなく、会合数の温度変化を示す微係数の項があるが、後に述べる相分離モデルのΔSoやΔHoにはこの項がないので、留意しておくことがのぞま しい。)
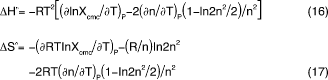
以上、会合数nが加わった項が複雑な姿で現れた式であるため、 ここまで読み進まれた読者はいささかうんざりさせられたかもしれない。これまで論じて来たミセル形成の理論は、n個の活性剤分子が集合して出来たミセルMなるものをあたかも一つの化学種が生じたものとみなす立場に立っている。すなわち、化学平衡論からみた‘生成物としてのミセル’を取扱っているので、このモデ ルを質量作用モデル(Mass Action Model, MAM)という。
1.3. ミセルを相(phase)とみなすときのミセル形成論
― Phase Separation Model
MAMに対して、ミセルを一種の相(phase)とみなす考え方 がある。もっともミセル形成を相の発現とするとGibbsの相律に矛盾するので、偽(擬)相(pseudo phase)と呼んでいる。先ず非イオン性の活性剤の方から述べよう。これによると、溶液相 (Bulk相とも言う)とミセル相の成分i(溶媒である水を1とし、 非イオン性の活性剤種をi = 2, 3…とする)の化学ポテンシャルがμis とμimで表されるとすると、定温・定圧の相平衡の状態では次式の関係が成立つはずである3)。
![]()
簡単のため、単一成分2だけからなる系を考える。その場合には、 ミセル相中の化学ポテンシャルは一定であるから、ミセルの化学 ポテンシャルを表す式 : μis=μim,o (T,P)+RTlna2m において、ミセルの活量をa2m = 1とおけるので、μis=μim,o (T,P)となる。単分散状態の溶液相では μis=μis,o (T,P)+RTlna2s で表せる。(ただし活性剤の活量a2s はモル分率x2sと活量係数 f2s の積である。)
活性剤2の1molがミセル形成するときのGibbsエネルギー変化をここではΔGmとし、標準自由エネルギー変化を ΔGmoとする。
![]()
平衡状態ではΔGm = 0であるから、結局、次式が得られる。
![]()
ここでa2sがconst. (T, P)であることがわかる。
一方Gibbs エネルギー変化は、ΔGm =ΔHm - TΔSm 及びΔGmo = ΔHmo - TΔSmo で表現できる。ΔHmとΔHmo 及びΔSmとΔSmoとの相違について以下述べてみよう。
ここでミセル形成に関して、下に示すようなエネルギーサイク ルを考えることにする。与えられたTとPのもとで、先ず完全に水和した単量体だけが100%存在する状態(x2s = 1)を仮想的に標準状態1(μ2s=μ2s,o)とする。Bulk相中で水和している単分散状態の単量体が状態3 (μ2s=μ2s + RTlna2)を経て、ミセルを形成し、ミセル(標準状態2とする)と単分散の水和活性剤分子が平衡状態に達するものと考える。したがって、標準状態1から標準状態2へ移行する熱力学量ΔGmo 、ΔHmoおよびΔSmoは仮想的なものを含んでいる。(次のダイアグラム参照)。標準状態1から状態3へ の移行はエントロピー項だけの寄与によると考えてよい 3)。
さて、式(20)のΔGmoに戻ってみると、CMC以上の濃度にお いても、a2sが一定であるということを示している。また、CMC 前後の濃度は一般に希薄であり、理想性を仮定することが許され るので、a2s = x2s = [CMC]とおける。ここで、前節まで用いて来たように問題にしている非イオン性活性剤のCMCをモル分率 Xcmcで表すと、式(20)は
![]()
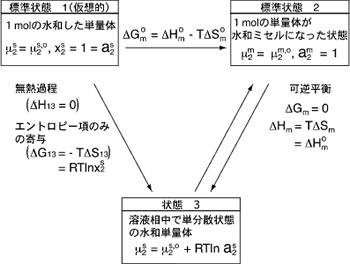
ここで、この(擬)相分離モデル (Phase Separation Model, PSM)におけるCMCとは即ち、「ミセルの溶解度」とみなしてよ いことがわかるであろう。
式(21)をもとに各熱力学量は次のように与えられる 3)。
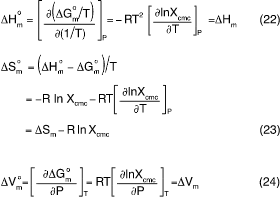
ここでΔSmとΔVmはΔGm = ΔGmo - RTlnXcmcの全微分をとって、(∂ΔGm /∂P)T = ΔVm 及び、(∂ΔGm/∂T)P = -ΔSm であること、及びΔHm = TΔSm であることから上式の関係が導かれる。(注意すべきは、式(24)において相分離モデルでは ΔVmo =ΔVm が上記の様に成立つが、質量作用モデルではΔVmo ≠ΔVmである。特に圧力が高くなるほどその差は大きくなる 20)。)
以上はPSMにおける非イオン性活性剤に関する熱力学量の関係 を示した。
次にイオン性活性剤を以前と同様に1-1電解質Na+、S- についてPSMの立場から各熱力学量は、簡単に次のように示すことがで きる。ここでも1個のミセルはn個の活性剤分子の集合体であり、 ミセル表面にはn・β個の反対イオンが結合しているものとする。標準Gibbsエネルギー変化は式(25)で示される。
![]()
この式から二つのことが言える。一つはCMCの対数値を反対イ オン濃度の対数値に対してplotする。すなわちCorrin-Harkins Plotをすると、その直線関係の傾きが反対イオン結合度 β に対応するという、式(9)と同じものであることである。他の一つは、 CMC近傍においてミセルの数は少ないので式(25)はΔGmo/RT=ln XcmcXNa+βとおけること、即ち、[CMC][CMC+添加塩]β の積が添加塩濃度に依ることなく一定である。これは「CMCをミセ ルの溶解度とみなせる」と上でも述べたが、溶解度積一定の法則に相当することがらである3)。
著者らはかつて、ナトリウム石鹸のような弱酸(脂肪酸)と強塩基(NaOH)からなる活性剤のミセル形成には、CMCがpHにも強く依存し、Na+ ばかりでなくH+もまた反対イオンとして結合(すなわち和水分解度は単分散状態よりもミセル形成状態の分子の方が大きい)することを見出し、それぞれの反対イオン結合度を βNa 及び βH で表し、-log[Na+]をpNaとすると
![]()
の関係が成立つことを胆汁酸塩の例で実験的に示した 21)。
添加塩がないとき、式(25)のX Na+ はXcmc に等しいから次式が得られる。
![]()
この式は、イオン性活性剤のミセル形成を熱力学的に論じるときに必ず登場してくる。
ΔHm , ΔSm について添加塩のないときは :
![]()
であり、また、添加塩があるときは :
![]()
である3)。
1.4. 両モデルの比較
ミセルを一種の生成物とみて取扱うMAMと、擬(偽)相とみなして取扱うPSMについて熱力学量を比較しながら考えてみよう。
イオン性活性剤について両モデルの式、すなわち式(12)と式 (26)を比べると、MAMには会合数の項があるが、PSMにはそれがなく、極めて簡単である。非イオン性については、ある程度会合数が大きいものと仮定した場合でさえ、MAMには会合数の項が残っているが、PSMでは式(21)でみるように、nに関係した項がない。
次に非イオン性活性剤のΔHo や ΔSoに到ってはMAMでは会合数の温度依存性の項があるが[式(16)と式(17)]、PSMには、n の温度依存性は無視したかたちになっている[式(22)と式(23)]。 これは、nの値そのものがさほど小さくないが、温度変化 (∂n/∂T)Pが無視できない系では、両モデルから見積られるそれらの値にかなりの相違が出て来よう。体積変化ΔVoについては (∂n/∂P)Tの項が含まれる5) 。
イオン性の界面活性剤のΔHo (ΔHm), ΔSo (ΔSm) 及びΔVo (ΔVm)などでは、MAMの場合には、会合数関連の項に加えて( ∂β/∂T)P 項がエンタルピーとエントロピーに含まれる[式(13)と式(14)] 5)。ΔVoには (∂β/∂P)Tが無視できない量で加って来ることが議論されている20)。
以上にみて来たように、MAMの方がPSMよりも精確度の高いものと判断できる。PSMはミセルを擬相として簡便に扱える代りに、熱力学的厳密さに欠けるものである3-5) 。しかし、実際場面では、会合数nを各温度で求めたり、反対イオン結合度の温度変化 や圧力変化をいちいち決めて行くには苦労を伴う。
ここで、MAMの各熱力学式をよく観てみよう。nが充分に大き いとき(数十以上)nに関わる項は第一項に比べて無視しうるほど に小さいものとなる。
したがって、会合数の大きい場合のGibbs エネルギー値は、MAM、PSM共によく一致するようになる。しかし、 ΔHoやΔSoの見積にあたっては (∂n/∂T)Pや(∂β/∂T)Pの項を、無視できな いのと同様にΔVoについても、先に述べたように( ∂β/∂P)Tの項の他に、会合数の圧力変化(∂n/ ∂P)Tの項も無視できないこと20) を繰返し注意しておく。
2. 濃度・圧力・温度の三変数で示す界面活性剤/水系の状態図
上の節で界面活性剤分子が集合してミセル形成をする際の熱力学的側面の骨子を述べて来た。しかし、活性剤は濃度(C)のみならず、温度(T)や圧力(P)によってその溶存状態は変ってく る(一般の物質が固・気・液体の三態をとると同様に)、状態を記 述するこれらC, T, Pを関数として活性剤水溶液系の全体像を眺めることも重要である。
2.1. 曇点、Krafft点及びCMCの決定法
この問題に立入る前に、非イオン性活性剤の多くにみられる曇 点(cloud point)現象やイオン性活性剤にみられるKrafft点(Krafft point)などの簡単な説明や、CMCの決定法などについて触れておこう。
非イオン性活性剤の代表的なものとしてpolyoxyethylene alcohol類(炭化水素鎖長をCn 、オキシエチレン鎖長をEmで示し、Cn Emと略表記される)が挙げられる。これらは温度の上昇と共に CMCは低下して行く一方22)、会合数が増大して行き 22~24)、ついには二相に分離して溶液は急濁する。この温度を曇点という。曇点は温度を徐々に上昇させながら、目視によって検知できる。一旦濁った溶液を冷却しながら透明になる温度も観測して、両者を平均して表示するのが普通である。
曇点は濃度に若干依存性があるので、測定時の濃度を示しておくことが必要である。ここで注意しておくべきこととして、曇点 現象は非イオン性活性剤すべてに共通な性質ではないことである。 MEGA-8, -9, -10等のN-methyl-glucamine系やn-nonyl-β-D thiomaltoside(これらはいずれも膜蛋白可溶化剤として利用されている)など、図2 (a)に示すように糖由来の水酸基が多数含まれる親水基を持つ非イオン性活性剤は、100℃近くまで熱しても曇点 現象は観察されない。むしろ、CMCの温度依存性を調べてみる と、温度の上昇と共にCMC値は低下するが、ある温度で極小を経て増大する現象がみられる25), 26)(MEGA-10については、CMC-温度曲線に極小がみられず、わずかながら単調に減少するだけであったとする、現著者との共同研究の報告もある 27)。)面白いことに、CnEm 型の活性剤(m = 10, n = 10, 16)とMEGA-10を混合すると曇点が著しく高くなり、ミセル溶液の温度領域が大きく広げられることが分かった27)。
イオン性活性剤の固体からミセル溶液へ転移する温度の観測は、 曇点と同様に目視でも可能な場合もあるが、電気伝導度法による ものが一番確実である。これには、所定量の活性剤が投入された 溶液の温度を徐々に上昇、または降下させながら、電気伝導度の変化を追跡して行き、伝導度の急変を生じる温度をもって、逆にその温度に於ける溶解度は仕込んだ活性剤の濃度とする方法があ る。一方設定温度ごとに、濃度対伝導度の関係を求めて、描く曲 線の屈折を与える濃度を、その設定温度における溶解度とする方法の二つがある。前者は固体⇔ミセル溶液間の溶解度決定に、後 者は固体⇔単分散間の溶解度決定にそれぞれ適している 28), 29)。温度一定のもとで圧力を変数としてイオン性活性剤の溶解度(及び CMC, 後述)を調べたTanakaら30-32)やIkawaら 33)の研究があるが、これも電気伝導度法を応用している。
次にCMCの決定法についてそのあらましを述べる。
イオン性、非イオン性を問わず、最も広く応用されているのが、 表面張力法で、図1に示すような表面張力対対数濃度の屈曲点を 与える濃度をCMCとする。表面張力測定法にはDu Nouy式円環法、Wilhelmy式平板法のほか液滴の体積を測る滴容法や、質量を 測る滴重法がある。滴容法による精密な表面張力測定を基に、 Aratono34)やMotomura35)らが厳密な熱力学を、活性剤の界面吸着やミセル形成について単独系ばかりでなく混合系に関してまで深く広く展開している。ここでは詳述を避けるが、参照に値する研究例が多数みられる。
イオン性活性剤のCMC決定に最も好都合なものは電気伝導度法である。比電導度法(κ)対濃度(C)のplotをすると、CMC
以上で勾配が急変するので、低濃度側から引いた直線と高濃度から引いた直線の交点を与える濃度をCMCとする(図3参照)。ここで得られる2直線の勾配の比を反対イオン結合度
βと関係ある量として36)、あるいはそのものに等しい
37~39)とみなしている報告がある。また、モル電導度Λ(
=K/C)対 ![]() の plotでもCMC以上でΛ値が急激に低下するので、その低下開始点の濃度をCMCとすることができる。さらに微分電導度dk/dCをCに対して
40)、あるいは
の plotでもCMC以上でΛ値が急激に低下するので、その低下開始点の濃度をCMCとすることができる。さらに微分電導度dk/dCをCに対して
40)、あるいは![]() に対してplotしてCMCを直接に決められる
18),40),41)。またdk/dC対
に対してplotしてCMCを直接に決められる
18),40),41)。またdk/dC対![]() のデータからミセルの解離度
α(
のデータからミセルの解離度
α(![]() 1-β)を見積もる議論をしている18),42) 。その他のCMC決定法5)としては、吸光度(適当な吸収があるとき)、濁度法又は光散乱法
43)、可溶化法44)、屈折率法、電位差法、蒸気圧法、音速法及び粘度法などがある。
1-β)を見積もる議論をしている18),42) 。その他のCMC決定法5)としては、吸光度(適当な吸収があるとき)、濁度法又は光散乱法
43)、可溶化法44)、屈折率法、電位差法、蒸気圧法、音速法及び粘度法などがある。
ここで注意すべきは、同じ条件下の同じ溶液についても得られ
るCMC値が用いる方法によって異なる(例えばκ対cとΛ対 ![]() は多少異なる結果を導く)ということである。一般に単分散種に由来する物性(例、表面張力降下)から求めたCMC値は、活性剤
ミセルに由来する物性(例、濁度)から得た値に比べて小さめに出ることが知られている5)。正確にCMCを定義した上で、正しく
CMCを決定するためには、Philipsの定義45)
に従うのが最良であるとMoroiは強調している5), 46)。ここでPhilipsの定義とは、溶液のある物理化学的性質φが、活性剤濃度[S]とミセル濃度[M]と関
係づけられ、
は多少異なる結果を導く)ということである。一般に単分散種に由来する物性(例、表面張力降下)から求めたCMC値は、活性剤
ミセルに由来する物性(例、濁度)から得た値に比べて小さめに出ることが知られている5)。正確にCMCを定義した上で、正しく
CMCを決定するためには、Philipsの定義45)
に従うのが最良であるとMoroiは強調している5), 46)。ここでPhilipsの定義とは、溶液のある物理化学的性質φが、活性剤濃度[S]とミセル濃度[M]と関
係づけられ、
![]()
で表されるとして、φを活性剤総濃度Ctに対してplotしたとき、 得られる曲線の勾配が最も大きく変化するところの濃度をCMCとする。すなわち、次の関係が得られるところとする。
![]()
たとえば、比電導度κがφに相当する例については、図3に示すようにd2k/dCt2が極小となり、d3k/dCt3が0となる濃度がCMCであるとする5)。ちなみにκvs Ct関係の交点附近で曲率のある曲線が現れるのは、CMC近くより単分散種のうち一部がミセル形成 し始めて、CMCに於てその値100%が単分散種ではなく、ほんの 一部はすでにミセルとして存在しているため、期待される単分散の寄与分(延長破線)より下に出る。その湾曲部分の曲率半径は、 会合数の小さいものほど大きい。CMCでは、会合数20のミセルで約2%、50のミセルで約1%がミセル化しており、それぞれ98 %及び99%が単分散状態にある5), 47)と計算されている。
2.2. 圧力と温度の関数としての物性―イオン性活性剤における Krafft温度(臨界溶解温度)とTanaka圧力(臨界溶解圧力)の関係
イオン性界面活性剤のCMCを温度に対してplotすると、ある温度で極小を示すことはよく知られている3), 5), 15), 16), 18), 41), 42)。 図2 (b)に例を示した。これに溶解度曲線を重ね合わせると、図4 (a)に見られるような二つの曲線の交叉がみられる。この系はSodium Perfluorodecyl Sulfate (SPFDe) の400atm下における状態図である。二つの曲線の交点を与える温度が400atmにおけるKafft 温度である。この温度を臨界溶解温度 (Critical Solution Temperature, CST)とも言う。
一方、図4 (b)も、定温55℃におけるSPFDe水溶液の状態図で、これは圧力Pを関数としている。圧力と共に上昇傾向にある P-CMC曲線と、水和固体からミセルへ転じる融解曲線(固⇔液の融解圧曲線に似ている)と水和固体から直接単分散状態に転じ る溶解度曲線の交点でP-CMC曲線も重なり、あたかも三重点のようにみえる(Krafft点に対応する交点もあたかも三重点のように みえる)。この交点を与える圧力は臨界溶解圧 (Critical Solution Pressure, CSP)であり、Tanaka圧力とも呼ばれる33), 49)。この二つの相図を温度T、圧力P及び濃度Cの関数として一つの立体 図にして表したものが図5である。
図5はイオン性界面活性剤水溶液の相状態を一般的に示したもので、圧力一定下のT-C相図では、下にトツのCMC曲線と溶解 度曲線の交点kを与える温度がKrafft温度を示している。また、温度一定下での断面では、上にトツのCMC曲線と溶解度曲線の交 点tがTanaka圧力を示している。点kからtへかけて臨界溶解曲線 (critical solution curve) に沿ってtに達し、さらにt-s-kの曲線で囲まれる曲面が、TとPを関数としたCMC曲面に相当する。水和固体相と単分散相を除く部分がミセル溶液相ということになる。ともあれ、図5はイオン性界面活性剤水溶液の三次元状態図である。
Krafft温度とTanaka圧力との間の関係が色々な活性剤について求められており、その例を文献4), 30), 31), 32), 33) から引用して図6に示す。Krafft温度は、圧力と共に高くなるとも言えるし、Tanaka 圧力は温度と共に上昇するとも言える。
3. 熱力学パラミターΔHmo、ΔS mo、ΔVmoなどの見積り
第1節ではミセル形成の化学熱力学式を示し、第2節では活性 剤水溶液物性を濃度、温度及び圧力の3示量変数の関数としてそ の概観を眺めて来た。ここでは、熱力学の式に基づいてミセル形 成に伴う種々の示量変数の変化、即ちエンタルピー、エントロピー 及び体積などの変化量について例を示しながら簡単に述べてみよ う。これらは、すべて第1節で述べたGibbsエネルギー変化の ΔGmoを基に解析して行くものである。
3.1. ΔHmoとΔSm o及びΔH-ΔS補償則
ΔHmoの見積りの基礎となる熱力学式は、Gibbs-Helmholtzの 式で与えられるものであり、第1節の式(13)、(16)及び(22)で示 した。上の1.5節で注意したように、厳密には非イオン性活性剤については会合数の温度変化を、またイオン性については会合数のほか反対イオン結合度βの温度依存性を無視できない。相分離モデルに基づいて、イオン性活性剤のβを一温度でのみ決めた値 を使って、式(26)に各温度のCMC値を代入してΔGmoを計算することに問題がある。このΔGmo値からミセル化熱ΔHm(=ΔHmo)を求めること、いいかえれば、lnXcmc 対1 / T のvan't Hoff Plotから得られる関係を直線とみなしてΔHmを決めることは芳しくない。 van't Hoff Plotから推定したΔHmと微少熱量測定から求めるミセル化熱は大きく異ることをKreshech50) らやPestman51) が警告して来ている。彼らは溶液の熱容量(ΔCP)の温度変化に並行して、ミセル化熱の温度変化が著しいことを示している。 ΔCPの変化は会合数nや反対イオン結合度βの変化に並行するものであるから、 ΔGmo/RT対1/Tのplotが単純な直線を与えるものではない。
図7にα-Sulfonatomyristic AcidのMethylとEthylのエステル(α-SMy・Me & Et)の例を示す。この活性剤は生物分解が容易で対硬水性にすぐれている 16), 18), 52)。アルキル基の鎖長をいろいろ変えてつくられており、 α-SFシリーズの名で総称されている52)。α-SFe・MeもEtも図2 (b)に示したように、各温度下でCMCと、それに加えてCMCに対する添加塩効果を調べ、Corrin-Harkins Plotによってβを求めた上でΔGmo をそれぞれの温度下で決めたものである。これにGibbs-Helmholtz Plot (我々はこのplotをvan't Hoff Plotと呼ばないことにしている)を施したのが図7の(a)で ある。βの温度変化を含んでいるのでこのplotは単純な直線になっ ていない。この接線勾配からΔHmo を求めたものが(b)に示してあり、さらにΔSmo = (ΔGmo -ΔHmo) /Tの関係から計算したミセル化のエントロピー変化が(c)に示してある。ここで求めた ΔHmoとΔSmo は、式(13)と(14)に於けるそれぞれの第三項、すなわち会合数に関する項のみを除外した、第一項と第二項をそれぞれの内容として包含しているものと考えられる。
さて、図7 (b)と(c)のエンタルピーとエントロピーの両方を見比べると、 ΔGmo を負にする(ミセル形成の自発性を高める)ためには不利となる ΔHmo > 0のところでは、ΔSmoが大きな正となっていることがみられる。言い換えれば、エンタルピー項が不利なとき、エントロピー項がこれをかばい(低温側)、逆にエントロピー 項の寄与が小さい場合、エンタルピー項がこれを補っている(高温側)ことがはっきりと認められる。これはエンタルピー・エントロ ピー補償則又は現象(Enthalpy-Entropy Compensation Rule or Phenomenon)と呼ばれるもので、水溶液系で生じる様々な変化・ 過程(生体系の諸過程を含めて)が観察されている53) 。種々相異る系に対してΔHをΔSに対してplotすると、一本の直線上に乗り、 その勾配が温度の次元をもつので補償温度と呼ばれている 53)。数多くの界面活性剤のミセル形成のこれらについても補償則が成立つことが報告されている50), 54), 56)。著者らはΔSmoをΔHmoに対してplotし、次の式で各活性剤にあてはまることを示した(図8)。
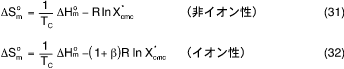
ここでTCは補償温度で 307 ± 8K の範囲にすべての活性剤が含められることがわかっている 56), 57)。また、-RlnX*cmc や -( 1 + β ) R lnX*cmc は ΔHm = 0 におけるエントロピー値に相当し、活性剤の種類によって異る。図8はそれぞれの化学種における各温度の ΔS -ΔH データが直線関係を成立たせているもので、このときのTCを自家補償温度(Self-compensation Temperature)と呼び、同一温度において相異る化学種同士について一本の直線関係が得られるときのTCを他家補償温度(Cross-compensation Temperature)とし、補償温度に関する詳細な議論を行っている 57)。
3.2. ΔVm又はΔVmo の見積り
着目する活性剤の状態変化にどの程度の部分モル体積の変化を伴うか、それを知ることは物性を論じる上で不可欠である。CMCの圧力変化を調べれば、ミセル形成に伴う体積変化ΔVm又はΔVmoが求められることを、第1節で、PSMの立場から式(24)で示し た。MAMでは、非イオン性及びイオン性活性剤についてそれぞれ次式で表される5)。
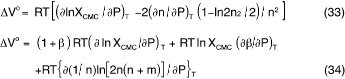
これらの式も既に述べて来たように、会合数nの圧力変化を求めることを要求しており、またイオン性については、たとえnが大 きくてnに関する項を無視出来るとしても、βの圧力依存性を知らねばならぬことを示している。
Kaneshinaらは、種々のSodium alkylsulfate(octyl、decyl、dodecyl、tetradecyl、それぞれSOS、SDeS、SDS、STS)についてCMCの圧力変化を35℃で求め、さらにSDSについては反対イオン結合度を Corrin - Harkins Plotより決め、Evansの式36)に電気伝導度のデータを代入して会合数nを各圧力で求めて いる58)。ここでイオン性活性剤の部分モル体積変化の見積りに基本となるCMC-圧力曲線をKaneshinaらのalkylsulfate系活性剤に加えて、著者らのSodium perfluorooctanoate(SPFO)の測定値20)をまとめて図9に示す。イオン性活性剤のミセル形成は常圧~約1000atm付近まで体積増(即ち、1molあたりのモル体積はミセルとなって集合した状態の方が単分散状態より大きい) ΔVm > 0を伴うので、Le Chaterierの原理によりCMCは高くなる。同時に、会合数が減少し、また反対イオン結合度βも減少(ミセルの解離度αが増大)をすることが確かめられている 58)。CMCがある圧力で極大をとり、そこでΔV m = 0となり、これより高い圧力下ではΔVm<0であることが、次のKaneshinaらが用いた式をみれば理解できよう。
![]()
CnEm型の非イオン性活性剤のCMCも千~千数百気圧で極大をとり、一方で会合数が圧力と共に減少することやΔVm が正から負に転ずることなどを、Laser光散乱法によってNishikidoらが確かめている59)。図9は、炭化弗素系活性剤のSPFOが群を抜いて ΔVmが大きいことを示唆している。
Ikawaら33)は、図4 (a)に示す溶解度-圧力及びCMC-圧力曲線を解析してSPFDeの単分散状態からミセル化に伴う部分モ ル体積変化ΔVmと、単分散と水和固体状態の差、すなわち結晶化の部分モル体積変化ΔVC = VC - VS を次式を適用して求めた(図10)。
ここでCSは溶解度である。図10には比較のために、Tanakaら のSDSのデータ33)とMukerjeeらのSPFOのデータ 20)を加えている。炭化水素系活性剤と炭化弗素系の体積変化挙動を比較すると、後者の方がはるかに顕著である。SPFOとSDeSとはCMC 値はほぼ同じであるにも拘らず、1atmにおけるΔVm 値は前者の方が倍近く大きい理由を疎水性水和の強さやミセル形成の定圧熱 容量変化ΔCPの大きさを用いてうまく説明している 20)。
終りに
以上、ミセル形成のみに的を絞って、その基礎的な熱力学を論 じて来た。
![]()
界面活性剤の他のもう一つの重要な性能は、界面吸着 とそれに伴う界面張力の降下であり、可溶化や乳化の特異な機能 が挙げられるが、ここでは論じることを控えた。また、濃度領域によって、会合状態が変り複雑な相挙動をする様子も深く研究さ れているが、これの紹介も省略した。
さらに重大な着目点は、界面活性剤の混合効果である。活性剤混合系は、異分子間の相互作用のあり方に興味深い挙動をみせ、混 合による相乗効果によって、それぞれ純系とは大いに異る性能を示すことがみられるので、多数の研究がなされている。混合系を 研究してみると、尽きることのない興味が湧いて来るものである。
本総説では紹介しなかったが、最近Tsujiiによって“Surface Activity”なる著書が刊行された60)。基礎事項を判り易く説明し、最 新の重要知見を織り混ぜたこの良書を参照するのも有益であろう。
著者らの研究に対し、惜しみなく支援を賜ったライオン(株)、 塩野義製薬(株)、三菱東京製薬(元東京田辺製薬)(株)、三栄源 FFI(株)、ならびに、(株)同仁化学研究所に深い感謝の意を表し ます。
参考文献
1) 嶋林三郎・寺田弘・岡林博文編集,「生態コロイドI」廣川書店,
東京, (1990), 2章2節
2) K. Shinoda, T. Nakagawa, B. Tamamushi and T. Isemura, "Colloidal Surfactants",
Academic Press, New York and London (1963).
3) 松浦良平・近藤保編集「応用コロイド科学」廣川書店, 東京,
(1969), 8章(田中満分担執筆)
4) 田中満(a)油化学, 34, 206 (1985)(b)油化学, 34, 296
(1985).
5) Y. Moroi, "Micelles", Plenum, New York (1992)
6) G. Sugihara and M. Hisatomi, J. Jpn. Oil Chem. Soc., 47, 661
(1998).
7) Y. Moroi, J. Colloid Interface Sci., 122, 308 (1988).
8) M. L. Corrin, W. D. Harkins, J. Am. Chem. Soc., 69, 683 (1947).
9) M. E. Hobbs, J. Phys. Chem., 55, 675 (1951).
10) M. J. Schick, J. Phys. Chem., 68, 3585 (1964).
11) M. F. Emerson, A. Holtzer, J. Phys. Chem., 71, 1898 (1967).
12) E. J. R. Sudholter, J. B. F. N. Engberts, J. Phys. Chem., 83,
1854 (1979).
13) H. N. Singh, S. Swarup, S. M. Saleem, J. Colloid Interface Sci., 68,
128 (1979).
14) Y. Moroi, Y. Sakamoto, J. Phys. Chem., 92, 5189 (1988).
15) G. Sugihara, Y. Arakawa, S. Lee, Y. Moroi, J. Colloid Interface Sci., 170,
399 (1995).
16) M. Fujiwara, T. Okano, T. ミH. Nakashima, A.A. Nakamura, G. Sugihara, Colloid
Polym. Sci., 275, 474 (1997).
17) Y. -I. Araki, T. Yanagida, M. Hisatomi, T. Kiyota, S. Lee, and G. Sugihara, J.
Jpn. Oil Chem. Soc. 48, 307 (1999).
18) A.A. Nakamura, M. Hisatomi, G. Sugihara, M. Fujiwara, and T. Okano, J. Surf.
Sci. Technol., 14, 23 (1998).
19) M. Hisatomi, M. Abe, N. Yoshino, S. Lee, S. Nagadome, and G. Sugihara, Langmuir,
16, 1515 (2000).
20) G. Sugihara, and P. Mukerjee, J. Phys. Chem. 85, 1612 (1981).
21) G. Sugihara and M. Tanaka, Bull. Chem. Soc. Jpn., 49, 3457
(1976).
22) A. Malliaris, J. L. Moigne, J. Sturm and R. Zana, J. Phys. Chem. 89,
2709 (1985).
23) M. J. Shick, "Nonionic Surfactans", Dekker, New York (1964).
24) W. Brown, R. Johnson, P. Stilbs, and B. Lindman, J. Phys. Chem. 87,
4548 (1983).
25) M. Okawauchi, M. Hagio, Y. Ikawa, G. Sugihara, Y. Murata and M. Tanaka, Bull.
Chem. Soc. Jpn. 60, 2718 (1987).
26) H. Oda, S. Nagadome, S. Lee, F. Ohseto, Y. Sasaki and G. Sugihara, J. Jpn.
Oil Chem. Soc (Nippon Yukagaku kaishi), 46, 559 (1997).
27) S.B. Sulthana, P. V. C. Rao, S, G, T. Bhat, T. Y. Nakano, G. Sugihara, and A.
K. Rakshit, Langmuir, 16, 980 (2000).
28) H. Furuya, Y. Moroi and G. Sugihara, Langmuir, 11, 774 (1995).
29) G. Sugihara, S. Nagadome, T. Yamashita, N. Kawachi, H. Takagi and Y. Moroi, Colloids
Surfaces, 61, 111 (1991).
30) M. Tanaka, S. Kaneshina, T. Tomida, K. Noda and K. Aoki, J. Colloid
Interface Sci., 44, 525 (1973).
31) M. Tanaka, S. Kaneshina, G. Sugihara, N. Nishikido and Y. Murata in
"Solution Behavior of Surfactants", Eds. K. L. Mittal and E. J. Fendler, Vol. 1,
Plenum, New York (1982).
32) N. Nishikido, H. Kobayashi and M. Tanaka, J. Phys. Chem. 86, 3170
(1982)
33) Y. Ikawa, S. Tsuru, Y. Murata, M. Okawauchi, M. Shigematsu and G. Sugihara, J.
Solution Chem., 17, 1251 (1988).
34) (a)M. Aratono, A. Ohta, H. Minamizawa, N. Ikeda, H. Iyota and T. Takiue, J.
Colloid Interface Sci., 217, 128 (1999).(b)H. Iyota, N. Todoroki, N. Ikeda, K.
Motomura, A. Ohta, and M. Aratono, J. Colloid Interface Sci., 216, 41
(1999).(c)M.Aratone, M.villeneuve, T.Takiue, N.Ikeda and H.Iyota, J.Colloid Interface
Sci., 200, 161(1998).
35) (a)K. Motomura, S-I. Iwanaga, M. Yamanaka, M. Aratono, and R.
Matumura, J.Colloid Interface Sci., 86, 151 (1982).(b) K. Motomura, Y.
Yamanaka, and M. Aratono, Colloid Polym. Sci., 262, 948(1984).
36) H. C. Evans, J. Chem. Soc., 579 (1956).
37) P. Lianos and J. Lang, J. Colloid Interface Sci., 96, 222 (1983).
38) K. Tamaki, K. Kobayashi, T. Nomura, M. Iijima, and M. Shimoi, J. Jpn. Oil
Chem. Soc., 46, 209 (1997).
39) (a) I. Satake, T. Fukunaga, T. Maeda, and K. Hayakawa, Bull. Chem. Soc. Jpn.,
66, 1618 (1993).(b) I. Satake, T. Morita, T. Maeda, and K. Hayakawa, Bull. Chem.
Soc. Jpn., 70, 761 (1997).
40) M. Manabe, H. Kawamura, A. Yamashita and S. Tokunaga, J. Colloid Interface
Sci., 115, 147 (1987).
41) M. Fujiwara, T. Okano, T-H. Nakashima, and G. Sugihara, Colloid Polym. Sci.,
275, 474 (1997).
42) G. Sugihara, A.A. Nakamura, T-H. Nakashima, Y-I. Araki, T. Okano, and M.
Fujiwara, Colloid Polym. Sci., 275, 790 (1997).
43) M. Okawauchi, M. Hagio, Y, Ikawa, G. Sugihara, Y. Murata, and M. Tanaka, Bull.
Chem. Soc. Jpn., 60, 2718 (1987).
44) G. Sugihara, K. Yamakawa, Y. Murata, and M. Tanaka, J. phys. Chem., 86,
2784 (1982).
45) J. N. Philips, Trans Faraday Soc., 51, 561 (1955).
46) Y. Moroi and R. Matuura, Bull. Chem. Soc. Jpn., 61, 333 (1988).
47) J. E. Denoyers, G. Caron, R. Delisi, D. Roberts, A. Raux, and G. Perron, J.
Phys. Chem., 87, 1397 (1983).
48) P. Mukerjee, K. Korematsu, M. Okawauchi, and G. Sugihara, J. phys. Chem.,
89, 5308 (1985).
49) E. Kissa, in "Fluorinated Surfactants", Sarfactant. Sci. Ser. Vol.
50, Marcel Dekker, New York, 1994.
50) G. C. Kresheck and W, A, Hargraves, J. Colloid Interface Sci., 48,
481 (1974).
51) J. M. Pestman, J. Kavelam, M. J. Blandamer, and H. A. van Doren, Langmuir,
15, 2009 (1999).
52) Y. Yoneyama, J. Jpn. Oil Chem. Soc. (Yukagaku), 44, 2 (1995).
53) R. Lumry and S. Rajender, Biopolymers, 9, 1125 (1970).
54) V.C. Krishnan and L. H. Friedman, J, Solution Chem., 2, 37
(1974).
55) L. J. Chen, S-Y. Lin and C-C. Huang, J. Phys. Chem. B, 102,
4350 (1998).
56) G. Sugihara, and M. Hisatomi, J. Colloid Interface Sci., 219, 31
(1999).
57) G. Sugihara, T-Y. Nakano, S. B. Sulthana and A. K. Rakshit, Submitted for
publication in J. Oleo. Sci.
58) S. Kaneshina, M. Tanaka, T. Tomida and R. Matumura, J. Colloid Interface Sci.,
48, 450 (1974).
59) N. Nishikido, M. Shinozaki, G. Sugihara, and M. Tanaka, J. Colloid Interface
Sci., 82, 352 (1981).
60) K.Tsujii,“Surface Activity ” ,Academic Press, San Diego.London(1998)
| プロフィール | |
|---|---|
| 氏 名 | 杉原 剛介 (Gohsuke sugihara) |
| 福岡大学理学部教授・理学博士 | |
| 連絡先 | 〒814-0180 福岡県福岡市城南区七隈1-19-8 |
| 福岡大学理学部化学科基礎化学研究室 | |
| TEL 092(871)6631 ext.6215 FAX 092(865)6030 | |
| e-mail sugihara@cis.fukuoka-u.ac.jp | |
| 昭和11年11月18日広島市にて出生。昭和35年防衛大学校応用物理 学科卒業。陸上自衛隊勤務を経て昭和45年九州大学大学院理学研究科 化学専攻修士課程修了。同年4月から福岡大学勤務。昭和57年より現 職。その間、ウィスコンシン大学客員教授。 | |
| 主な著書 | 『改訂増補化学熱力学中心の基礎物理化学』 (学術図書、共著) |
| 『21世紀の大学基礎化学実験』 (学術図書、共著) | |
| 『三島由紀夫と自衛隊』 (並木書房、共著) | |